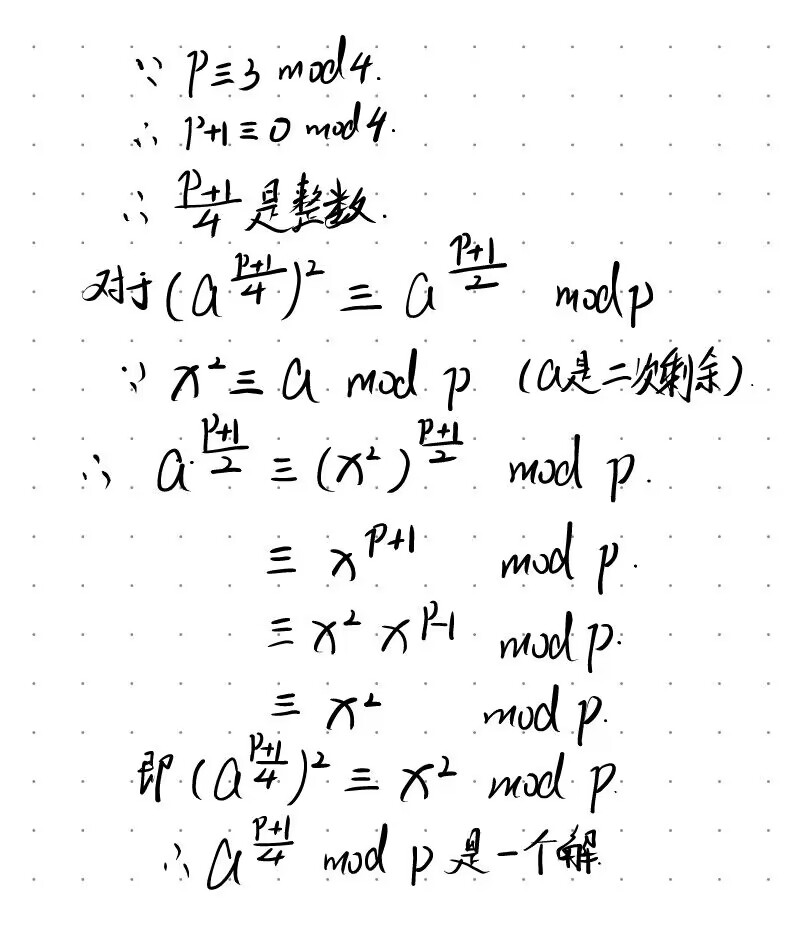椭圆曲线

下面进行椭圆曲线相关知识的学习（基于crypto hack），中间穿插了一些数论和近世代数的几个知识点。

一. 预备知识

学习的时候碰到了数论和近世代数的几个知识点，因为这两门我都没学完（尤其近世代数，完全没开始看），所有只能求尽量讲清楚吧。

群

近世代数是主要研究代数系统（即非空集合）的学科，我们会在这个非空集合上定义满足一定条件的一种或多种二元运算（代数运算）。群是近世代数里面一个重要的概念。下面放一个课本上的定义。

简单解释一下就是在一个非空集合里定义一个二元运算，这个运算对于这个集合内的元素都满足

(1)结合率 (2)单位元 (3)逆元

其实还有一个封闭性，就是运算结果还是在这个集合里。

举一个例子，对于所有非零有理数（非空集合），和普通乘法（二元运算）构成了一个群，这个群满足结合律（是显然的），有单位元1（任意数与1做这个二元运算都等于它本身，且交换也满足），且对于任意一个a，都有$ \frac{1}{a} $与a做这个二元运算后等于单位元1（交换也满足)

阿贝尔群（Abel 群）

阿贝尔群是在群的基础上加上一个条件得到的，即交换率

普通的群满足结合率，但是是不一定满足交换率的（目前我举不出具体例子，但是我是联想矩阵运算去理解的，不过可能不准确，感兴趣可以去查一下有没有具体例子）

所以一旦一个群满足交换律，这个群就是阿贝尔群，也叫交换群

交换群的概念在后面椭圆曲线的运算上会有比较重要的运用。一旦满足结合律和交换律，那么运算时的次序就没那么重要了，这是基于椭圆曲线的DH密钥交换的一个重要基础。

二次剩余

https://oi-wiki.org/math/number-theory/quad-residue/

是数论里面解同余方程那里的一个比较重要的概念，我们有以下定义：

令整数a，p满足（a，p）= 1，若存在x使得

$ x^{2} \equiv a\mod p $

则称a为模p的二次剩余，否则称a为模p的二次非剩余

这里面还是有挺多概念的东西的，但是上面博客里面讲的十分详细，可以看一看

所以这里我只强调一个特殊情况下的求解，即$ p \equiv 3\mod 4 $

满足上面所说情况，且我们知道a是p的二次剩余（怎么验证是不是二次剩余可以看看那个网站里，讲的很详细，数论我没学完，怕讲不清楚），就可以用下图方法来求一个解（可以求出x的值）

我们可以验证一下（自己推了一下，字有点丑，流泪猫猫）

这里因为p+1是4的倍数，指数部分就是整数，所以会很好算。大家也可以试试自己推一下加深理解

至于其他的情况我还没学完（流泪猫猫头），拜托，数论太难了，但是那个网站里面真的很详细！可以仔细研读

二. 椭圆曲线入门

https://www.cnblogs.com/Kalafinaian/p/7392505.html

要研究椭圆曲线就要知道维尔特拉斯方程（Weierstrass），这个方程的形式挺复杂的，感兴趣可以去查一下，然后我们主要运用它的普通形式，即

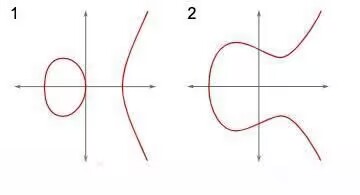
$ y^{2} = x^{3} +ax +b $

大致图像如下

像什么曲线每个点是非奇异的（光滑的）这样的性质我就不强调了，这里先知道长什么样就行

椭圆曲线上的点加法

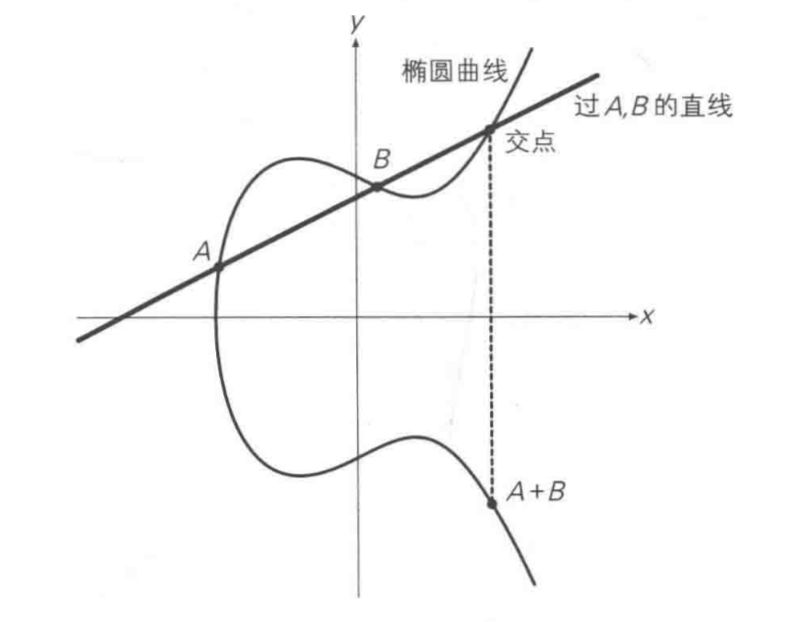
我们知道椭圆曲线长什么样子后，就会期望在上面做一些运算，而它确实也提供了点加法运算。其原理是

假设A=（x1，y1）B=（x2，y2）是曲线上的两个点

那么P + Q的结果，就是PQ连线与椭圆曲线的交点R‘关于x轴的对称点R，如下图

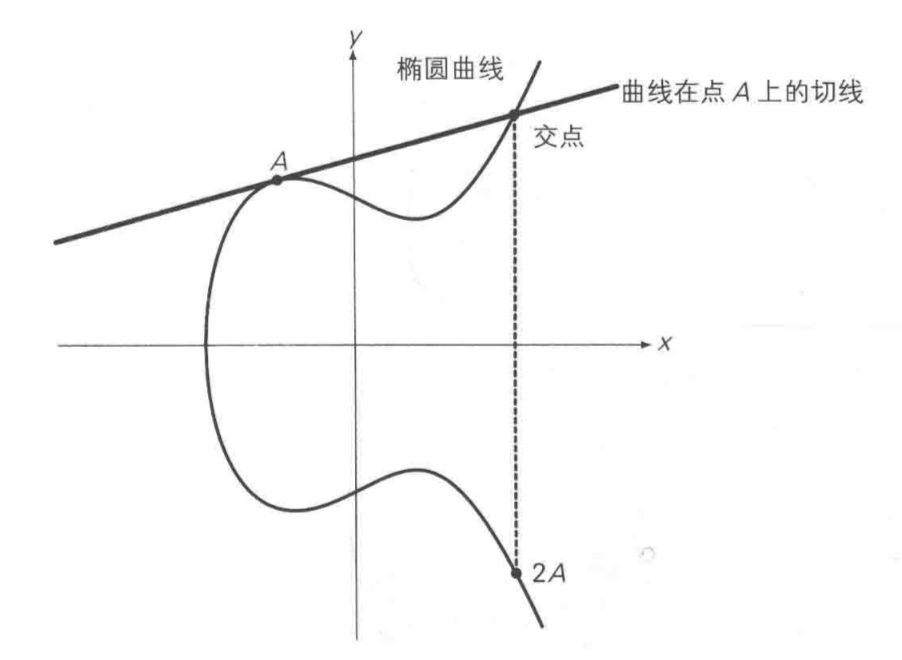
倘若是A + A，则我们考虑A点的切线，切线与椭圆曲线的交点R’关于x轴的对称点R即为结果，如下图

下面是一个具体的计算方法

单位元和逆元

我们知道了椭圆曲线上的点加法运算后，我们会期望它具备群属性，以便于我们研究，这就要找到一个单位元O，使得

$ P +O=P $

但我们会发现没有一个点是满足这个条件的，那么我们就规定一个无穷远处的抽象点为单位元O（可以想象一下，一个点和无穷远处点的连线与曲线的交点还是这个点，满足条件）。这个无穷远点可以看成在y轴的正（负）半轴的无穷远处。这就有了单位元了。

有了单位元后我们来找逆元，即存在-P使得

$ P +（-P）=O $

其实回顾一下点加法的定义，我们很容易就能找到逆元就是关于x轴对称的那个点

例如R=（x3，y3）那么逆元R’=（x3，-y3）

也可以想象一下，这两个点的连线就是交在无穷远处，满足定义。

到这里，椭圆曲线上的点加法满足了群的所以性质，所以满足椭圆曲线的所有点加上一个无穷大的虚数点O，就构成了一个群。实际是，这个群也是满足交换率的，而满足交换率的群我们称之为阿贝尔群。

然后我们真正研究的时候，其实会希望在一个有限域内去研究，特别是素数域，所有我们对方程取模，这样以后，我们研究的就是一些对称的点，而不是连续的线

取模后逆元那里就有点小区别因为-y = p - y mod p，所以在有限域上的逆元表示成 R’（x，p - y）

椭圆曲线构建离散对数问题（ECDLP）

对于一个给定的椭圆曲线E，考虑椭圆曲线上的两个元素P和T，DL问题就是找到整数d，使得

$ P+P+\dots+P =dP=T $

很多时候，这个d就是私钥（如在ECC加密体系里）

（d*P就是椭圆曲线上的标量乘法，不过理解上还是要当成点加法的重复进行）

很多时候，知道T来求d是十分困难的，相当于一个离散对数问题。这确保了椭圆曲线加密的安全性。

基于椭圆曲线的DH密钥交换

知道了椭圆曲线，我们要用来做一些和密码有关的事情

于是Alice和Bob协商做下面这些事

两个人并用分别用自己随机生成的整数a和b与P（公开）做标量乘法得到A（公开）和B（公开），并把得到的值分别传给对方。

Alice得到B并用自己一开始的那个随机数a与B做标量乘法，得到T，Bob同理。两人把得到的T作为共享密钥。

对于Alice：T = a （b P）

对于Bob： T = b （a P）

因为椭圆曲线是一个阿贝尔群，所以运算次序对结果不影响，所以两个人得到的T相同，这确保了交换的可行性

这个过程里面，外人只可能得到P、A和B（这三个是公开的），但是仅仅通过这三个是算不出a和b的（即算不出T），这确保了这个交换过程的安全性。

这样Alice和Bob就可以用这个联合密钥去加密一些东西

之后Alice和Bob进行了思考，他们认为，既然椭圆曲线方程已知，那干嘛还要传递y呀？（欸！我有一个好主意）于是他们觉得只传递x就可以了，以实现高效传递

事实上只传递x也确实是可行的，我们考虑把已知的x值代入曲线方程就可以得到 y² = k mod p 的形式

其中k是带入x后的算出值，这就是一个二次剩余问题（数论的知识点），这样就是一个比较简单解决的问题（课本上这么说的，虽然在我看来还是很难），很容易就可以求出y。

但这里会有一个小问题，那就是如果数对（x，y）满足上面那个式子，那么显然的（x，p - y）也是满足的，所以实际生活中，我们在传递x坐标时，会附带传递一个指定y的奇偶性的标志位，以此来达到区分到底是哪个点（感兴趣可以查一下，挺复杂的，没看懂）

三. 题目

Efficient Exchange

题目：

E: Y2=X3 +497X+1768 mod 9739

Calculate the shared secret after Alice sends you x(QA)=4726, with your secret integer nB=6534.

Use the file to decode the flag decrypt.py

{'iv': 'cd9da9f1c60925922377ea952afc212c', 'encrypted_flag': 'febcbe3a3414a730b125931dccf912d2239f3e969c4334d95ed0ec86f6449ad8'}

from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
import hashlib


def is_pkcs7_padded(message):
    padding = message[-message[-1]:]
    return all(padding[i] == len(padding) for i in range(0, len(padding)))


def decrypt_flag(shared_secret: int, iv: str, ciphertext: str):
    # Derive AES key from shared secret
    sha1 = hashlib.sha1()
    sha1.update(str(shared_secret).encode('ascii'))
    key = sha1.digest()[:16]
    # Decrypt flag
    ciphertext = bytes.fromhex(ciphertext)
    iv = bytes.fromhex(iv)
    cipher = AES.new(key, AES.MODE_CBC, iv)
    plaintext = cipher.decrypt(ciphertext)

    if is_pkcs7_padded(plaintext):
        return unpad(plaintext, 16).decode('ascii')
    else:
        return plaintext.decode('ascii')


shared_secret = ?
iv = ?
ciphertext = ?

print(decrypt_flag(shared_secret, iv, ciphertext))

考点：二次剩余，AES解密，ECDH的高效传递

这里主要考察对ECDH的高效传递的理解，Alice和Bob认为，椭圆曲线方程已知，那干嘛还要传递y呀？（欸！我有一个好主意）于是他们觉得只传递x就可以了。于是Alice给我发了一个x值，希望我能够以此知道共享密钥。并且Alice用共享密钥通过AES加密了flag

事实上只传递x也确实是可行的，我们考虑把已知的x值代入曲线方程就可以得到 y2 = k mod p 的形式

其中k是带入x后的算出值，这就是一个二次剩余问题（数论的知识点），这样就是一个比较简单解决的问题（课本上这么说的，虽然在我看来还是很难），很容易就可以求出y

不过这道题会相对简单，因为我们最后只用x来做文章，所以y的值我们不关心，那么对于同一个x，即使两个人最后算出来的y不一样（一个是y，一个是p-y），经过运算后也不会影响x的值（可能画个图会好理解一点，两个对称的点，画斜率，与曲线的交点的x还是一样的），所以我们任意求出一个y来进行计算就行

现在来进行y的计算，题目给了提示p = 3 mod 4，这就可以运用二次剩余的知识点来解决，下面是原理图

这里直接用

$ y = a^\frac{p+1}{4}\mod p $

当然你也可以直接遍历p（遍历完总能找到一个解），因为这题p确实不大，两个办法都行，都可以求p（我一开始用的第二个，觉得不是预期解法才去查的第一个），求出y了就没什么难度了，套那个解密文件就行。

# sage
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
import hashlib


def is_pkcs7_padded(message):
    padding = message[-message[-1]:]
    return all(padding[i] == len(padding) for i in range(0, len(padding)))


def decrypt_flag(shared_secret: int, iv: str, ciphertext: str):
    # Derive AES key from shared secret
    sha1 = hashlib.sha1()
    sha1.update(str(shared_secret).encode('ascii'))
    key = sha1.digest()[:16]
    # Decrypt flag
    ciphertext = bytes.fromhex(ciphertext)
    iv = bytes.fromhex(iv)
    cipher = AES.new(key, AES.MODE_CBC, iv)
    plaintext = cipher.decrypt(ciphertext)

    if is_pkcs7_padded(plaintext):
        return unpad(plaintext, 16).decode('ascii')
    else:
        return plaintext.decode('ascii')

p = 9739
y = int(((4726**3+497*4726+1768)**((p+1)//4))%p)
print(y)
E = EllipticCurve(GF(9739),[497,1768])
P = E([4726,6287])
shared_secret = (6534*P)[0]
print(shared_secret)

iv = 'cd9da9f1c60925922377ea952afc212c'
ciphertext = 'febcbe3a3414a730b125931dccf912d2239f3e969c4334d95ed0ec86f6449ad8'

print(decrypt_flag(shared_secret, iv, ciphertext))
 
# crypto{3ff1c1ent_k3y_3xch4ng3}

flag：crypto{3ff1c1ent_k3y_3xch4ng3}

四. 总结

到这里，我们对椭圆曲线就有了简单认识，但其实还并没有接触到真正的一些加密算法，比如说ECC（但是原理懂了这个也就很好理解了，所以问题不大）。而且椭圆曲线加密也不是绝对安全的，后面还要学习各种攻击方式（像之前我瞥到的光滑数攻击），总的来说，道阻且长。